1. kodowanie informacji
Kodowaniem nazywamy przyporządkowanie poszczególnym obiektom zbioru kodowanego odpowiadających im elemaentów zwanych słowami kodowymi.
Słowa kodowe czyli ciag 01 który nazywami jako kod. Przy czym każdemu słowu kodowemu musi odpowiadać dokładnie jeden element kodowany. Duża część informacji są to liczby binarne.
Liczby binarne czyli liczby logiczne, zero-jedynkowe, cyfrowe, dwójkowego
0 - brak przepływu prądu - tak zwane zero logiczne lub niski stan logiczny
1 - prąd w ukłądzie cyfrowym - tak zwana jedynka logiczna lub binarna lub wysoki stan logiczny
2. Przekształcanie systemu dziesiętnego na system binarny
| Liczba w systemie dziesiętnym | liczba w systemie binarnym |
| 0 | 00 |
| 1 | 01 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 (4+0+1) |
| 6 | 110 (4+2+0) |
| 7 | 111 |
| 8 | 1000 |
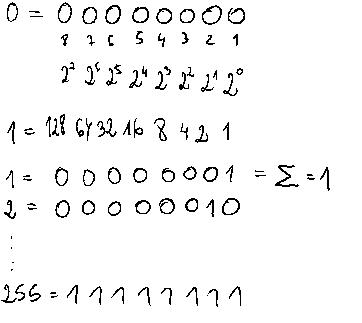system przeliczania liczb dziesietnych na liczby binarne
Powszechnie używany w elektronice cyfrowej, gdzie minimalizacja liczby stanów (do dwóch) pozwala na prostą implementację sprzętową odpowiadającą zazwyczaj stanom wyłączony i włączony oraz zminimalizowanie przekłamań danych. Co za tym idzie, przyjął się też w informatyce.
Jak w każdym pozycyjnym systemie liczbowym, liczby zapisuje się tu jako ciągi cyfr, z których każda jest mnożną kolejnej potęgi podstawy systemu.
Np. liczba zapisana w dziesiętnym systemie liczbowym jako 10, w systemie dwójkowym przybiera postać 1010, gdyż:
Przykłądy:
248 = 11111000 = 128 + 64 + 32 + 16 = 248
385 = 110000001 = 256 + 128 + 1 = 385
724 = 1011010100 = 512+128+64+16+4 = 724
927 = 1110011111
100 = 1100100
1000 = 1111101000
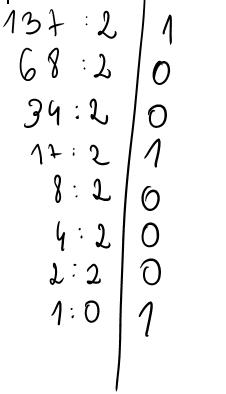
3. sposób przeliczania liczb binarnych w sposób dzielenia.
Konwersja liczby dwójkowej na liczbę dziesiętną
aby przeliczyć liczbę dwójkową na dziesiętną należy dodać kolejno wszystkie cyfry pomnożone przez wagę danej pozycji. zaczynamy od ostatniej cyfry.
137 = 10001001
